fm Factorization Machine - Rendle

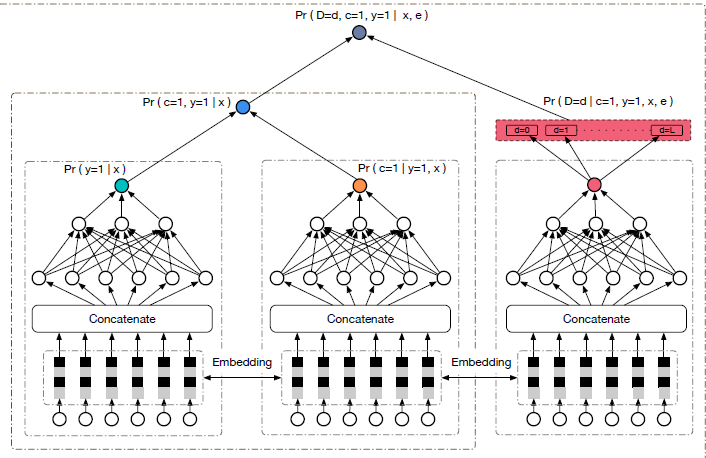
fm model

FM模型（因子分解机）是对Poly2的改进，以更好地处理数据稀疏性问题。此外，FM模型采用了矩阵因子分解技术，使其能够以近线性时间复杂度的高效性进行模型训练。对于每个特征，FM模型引入了一个维度为(k)的隐藏向量，其中(k)远小于特征数。因此，FM模型的模型方程如下：

The FM model (Factorization Machine) is an improvement over Poly2 to better handle data sparsity issues. Additionally, the FM model employs matrix factorization techniques, allowing it to train models with near-linear time complexity efficiency. For each feature, the FM model introduces a hidden vector of dimensions (k), where (k) is much smaller than the number of features. As a result, the model equation for the FM model is as follows:

[ \hat{y}(x) = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{j=i+1}^{n} \langle v_i, v_j \rangle x_i x_j ]

在这个方程中：

(\hat{y}(x)) 代表预测的输出。
(w_0) 是偏置项。
(w_i) 代表与第(i)个特征(x_i)相关的权重。
(v_i) 代表维度为(k)的第(i)个特征的隐藏向量。
(n) 是特征的总数。

FM模型的关键创新点在于第二个求和项，通过特征向量的内积高效地捕获了二阶特征交互。这使得模型能够捕捉特征之间的成对交互，而无需明确列举所有可能的特征对，从而适用于高效处理稀疏数据。

In this equation:

(\hat{y}(x)) represents the predicted output.
(w_0) is the bias term.
(w_i) represents the weight associated with the (i)-th feature (x_i).
(v_i) represents the (i)-th feature’s hidden vector of dimension (k).
(n) is the total number of features.

The key innovation of the FM model lies in the second summation term, which captures second-order feature interactions efficiently through inner products of feature vectors. This allows the model to capture pairwise interactions between features without the need to explicitly enumerate all possible feature pairs, making it suitable for handling sparse data efficiently.

FM (Factorization Machine) model’s principle

FM模型旨在以二阶多项式形式来近似特征之间的相互作用。对于给定的输入实例(x)，FM中的预测(\hat{y}(x))定义如下：

The FM model aims to approximate the interaction between features in a second-order polynomial form. For a given input instance (x), the prediction (\hat{y}(x)) in FM is defined as:

[ \hat{y}(x) = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{j=i+1}^{n} \langle v_i, v_j \rangle x_i x_j ]

下面是各项的详细说明：

(w_0) 是偏置项。
(w_i) 代表与第(i)个特征(x_i)相关的权重。
(v_i) 代表与第(i)个特征相关的潜在向量，具有(d)个维度（其中(d)是潜在向量的维度）。
(x_i) 是第(i)个特征的值。

Here’s the breakdown of the terms:

(w_0) is the bias term.
(w_i) represents the weight associated with the (i)-th feature (x_i).
(v_i) represents the latent vector associated with the (i)-th feature, with (d) dimensions (where (d) is the dimensionality of the latent vectors).
(x_i) is the (i)-th feature’s value.

现在，让我们专注于二阶交互项：

[ \sum_{i=1}^{n} \sum_{j=i+1}^{n} \langle v_i, v_j \rangle x_i x_j ]

这个项捕捉了特征之间的成对交互。内积(\langle v_i, v_j \rangle)表示潜在向量(v_i)和(v_j)之间的交互强度，而(x_i x_j)则捕捉了特征值(x_i)和(x_j)的乘积。

Now, let’s focus on the second-order interaction term:

[ \sum_{i=1}^{n} \sum_{j=i+1}^{n} \langle v_i, v_j \rangle x_i x_j ]

This term captures the pairwise interactions between features. The inner product (\langle v_i, v_j \rangle) represents the interaction strength between the latent vectors (v_i) and (v_j), and (x_i x_j) captures the product of the feature values (x_i) and (x_j).

这里的关键洞察是内积(\langle v_i, v_j \rangle)量化了潜在向量(v_i)和(v_j)之间的交互，从而反映了相应特征(x_i)和(x_j)之间的交互。这使得FM模型能够捕捉成对特征交互，而无需明确列举所有可能的特征对，使其成为一种高效且有效的方法，用于建模数据中的复杂关系。

The key insight here is that the inner product (\langle v_i, v_j \rangle) quantifies the interaction between the latent vectors (v_i) and (v_j), which in turn reflects the interaction between the corresponding features (x_i) and (x_j). This allows the FM model to capture pairwise feature interactions without the need to explicitly enumerate all possible feature pairs, making it an efficient and effective approach for modeling complex relationships in data.

损失函数

当涉及FM（因子分解机）模型时，损失函数和优化方法是关键组成部分。训练FM模型的目标是找到能最小化特定损失函数的模型参数。对于FM模型，用于二元分类问题的常用损失函数是逻辑损失（也称为对数损失或交叉熵损失），定义如下：

Certainly, for the FM (Factorization Machine) model, the loss function and optimization method are crucial components. The objective of training the FM model is to find the model parameters that minimize a certain loss function. In the case of FM, the commonly used loss function for binary classification problems is the logistic loss (also known as the log loss or cross-entropy loss), which is defined as follows:

[ \mathcal{L}(\Theta) = -\frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right] ]

这里是每个术语的含义：

(\mathcal{L}(\Theta))：逻辑损失，用于衡量一组(N)个训练示例的预测概率(\hat{y}_i)与真实标签(y_i)之间的差异。
(\Theta)：模型参数集，包括线性项的权重(w_0)和(w_i)，以及特征交互的潜在向量(v_i)。
(N)：数据集中的训练示例数。
(y_i)：第(i)个示例的真实标签（0或1）。
(\hat{y}_i)：第(i)个示例的正类别（类别1）的预测概率，它是通过FM模型(\hat{y}(x_i))的输出经过通过Sigmoid函数以确保其在范围[0, 1]内而得到的。

Here’s what each term represents:

(\mathcal{L}(\Theta)): The logistic loss, which measures the difference between the predicted probabilities (\hat{y}_i) and the true labels (y_i) for a set of (N) training examples.
(\Theta): The set of model parameters, including the weights (w_0) and (w_i) for linear terms and the latent vectors (v_i) for feature interactions.
(N): The number of training examples in the dataset.
(y_i): The true label (0 or 1) for the (i)-th example.
(\hat{y}_i): The predicted probability of the positive class (class 1) for the (i)-th example, which is the output of the FM model (\hat{y}(x_i)) after passing through a sigmoid function to ensure it falls in the range [0, 1].

为了优化FM模型，常用的优化算法包括梯度下降的变种，如随机梯度下降（SGD）、小批量梯度下降或Adam。目标是通过迭代地更新参数以减小损失来找到最小化逻辑损失(\mathcal{L}(\Theta))的模型参数(\Theta)。

To optimize the FM model, commonly used optimization algorithms include gradient descent variants like stochastic gradient descent (SGD), mini-batch gradient descent, or Adam. The goal is to find the model parameters (\Theta) that minimize the logistic loss (\mathcal{L}(\Theta)) by iteratively updating the parameters in the direction that reduces the loss.

具体的优化方法和超参数（学习率、批量大小等）取决于问题、数据集大小以及在训练速度和收敛之间所需的权衡。

The specific optimization method and hyperparameters (learning rate, batch size, etc.) depend on the problem, dataset size, and the desired trade-off between training speed and convergence.