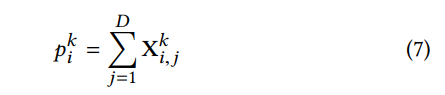xdeepfm 压缩交互网络（CIN）将CIN和经典的DNN结合 -中科大

摘要

组合特征对于许多商业模型的成功至关重要。

手动创建这些特征通常因网络规模系统中的各种原始数据的多样性、数量和速度而成本高昂。基于因子化的模型，它们通过向量乘积来衡量相互作用，可以自动学习组合特征的模式，并推广到未见特征。

随着深度神经网络（DNNs）在各个领域取得的巨大成功，近年来研究人员提出了几种基于DNN的因子化模型，用于学习低阶和高阶特征的相互作用。尽管DNN具有从数据中学习任意函数的强大能力，但普通的DNN在位级别上隐含生成特征相互作用。

在本文中，我们提出了一种新颖的压缩交互网络（CIN），旨在以显式的方式在向量级别上生成特征相互作用。

我们展示了CIN与卷积神经网络（CNNs）和循环神经网络（RNNs）具有一些相似功能。我们进一步将CIN和经典的DNN结合成一个统一的模型，并将这个新模型命名为eXtreme Deep Factorization Machine（xDeepFM）。

一方面，xDeepFM能够显式地学习某些有界度的特征相互作用；

另一方面，它可以隐式地学习任意低阶和高阶特征相互作用。我们在三个真实世界的数据集上进行了全面的实验。

我们的结果表明，xDeepFM优于最先进的模型。

model

我们设计了一个新的交叉网络，称为压缩交互网络（CIN），考虑了以下几个因素：

（1）交互作用在向量级别应用，而不是位级别；
（2）高阶特征交互作用被明确测量；
（3）网络的复杂性不会随着交互程度的增加而呈指数增长。由于嵌入向量被视为向量级别交互的单位，

因此我们将字段嵌入的输出形式化为矩阵X0 ∈ Rm×D，其中X0中的第i行是第i个字段的嵌入向量：X0i,∗ = ei，D是字段嵌入的维度。

第k层CIN的输出也是一个矩阵Xk ∈ R Hk×D，其中Hk表示第k层中的（嵌入）特征向量的数量，我们令H0 = m。对于每一层，Xk都是KDD’18，2018年8月19日至23日，英国伦敦的矩阵。

通过以下方式计算：

其中 1 ≤ h ≤ Hk，Wk,h ∈ R Hk−1×m 是第 h 个特征向量的参数矩阵，◦ 表示Hadamard乘积，例如，⟨a1, a2, a3⟩◦⟨b1, b2, b3⟩ = ⟨a1b1, a2b2, a3b3⟩。请注意，Xk是通过Xk−1和X0之间的交互导出的，因此特征交互作用是明确测量的，且随着层深度的增加而增加。CIN的结构与循环神经网络（RNN）非常相似，其中下一隐藏层的输出依赖于上一隐藏层和额外的输入。我们在所有层中保持嵌入向量的结构，因此交互作用在向量级别应用。

值得注意的是，方程式6与计算机视觉中著名的卷积神经网络（CNNs）有很强的联系。

如图4a所示，我们引入了一个中间张量Zk+1，它是隐藏层Xk和原始特征矩阵X0之间（沿着每个嵌入维度）的外积。然后，Zk+1可以看作是计算机视觉中的一种特殊类型的图像，而Wk,h则是一个滤波器。我们沿着嵌入维度（D）滑动滤波器，如图4b所示，得到一个隐藏向量Xk+1i,∗，通常在计算机视觉中称为特征图。

因此，Xk是Hk个不同特征图的集合。CIN名称中的“压缩”表示第k个隐藏层将潜在的Hk−1×m向量空间压缩为Hk个向量。

图4c提供了CIN架构的概述。让T表示网络的深度。每个隐藏层Xk，k ∈ [1,T] 都与输出单元连接。

我们首先对每个隐藏层的特征图应用总池化：

对于i ∈ [1, Hk]，我们有一个池化向量pk = [pk1, pk2, …, pkHk]，长度为Hk，对于第k个隐藏层。来自所有池化向量的池化向量如下：
在连接到输出单元之前，将所有隐藏层的池化向量连接在一起，形成一个汇总的池化向量p+ = [p1, p2, …, pT] ∈ R∑i=1 Hi。如果我们直接将CIN用于二元分类，输出单元将是p+上的一个S型节点：

公式表示为：

y = 1 / (1 + exp(p+^T wo)) (8)

CIN 分析

我们对提出的 CIN 进行分析，以研究模型复杂性和潜在有效性。

空间复杂性。第 k 层的第 h 个特征图包含 Hk−1 × m 个参数，这正好是 Wk,h 的大小。因此，在第 k 层有 Hk × Hk−1 × m 个参数。考虑到输出单元的最后回归层，它具有
∑k=1 Hk 个参数，CIN 的总参数数量为 ∑k=1 Hk × (1 + Hk−1 × m)。请注意，CIN 与嵌入维度 D 无关。相比之下，一个普通的 T 层 DNN 包含 m × D × H1 + HT +
∑ k=2 Hk × Hk−1 个参数，参数数量将随着嵌入维度 D 的增加而增加。

通常情况下，m 和 Hk 不会非常大，因此 Wk,h 的规模是可以接受的。必要时，我们可以利用 L 阶分解，并用两个较小的矩阵 Uk,h ∈ R Hk−1×L 和 Vk,h ∈ R m×L 替代 Wk,h： Wk,h = Uk,h (Vk,h)^(T) (9)

其中 L ≪ H 且 L ≪ m。此后，为了简化起见，我们假设每个隐藏层具有相同数量（即 H）的特征图。通过 L 阶分解，CIN 的空间复杂性从 O(mTH2) 降低到 O(mTHL + TH2L)。相比之下，普通 DNN 的空间复杂性为 O(mDH + TH2)，它对字段嵌入的维度（D）敏感。

架构

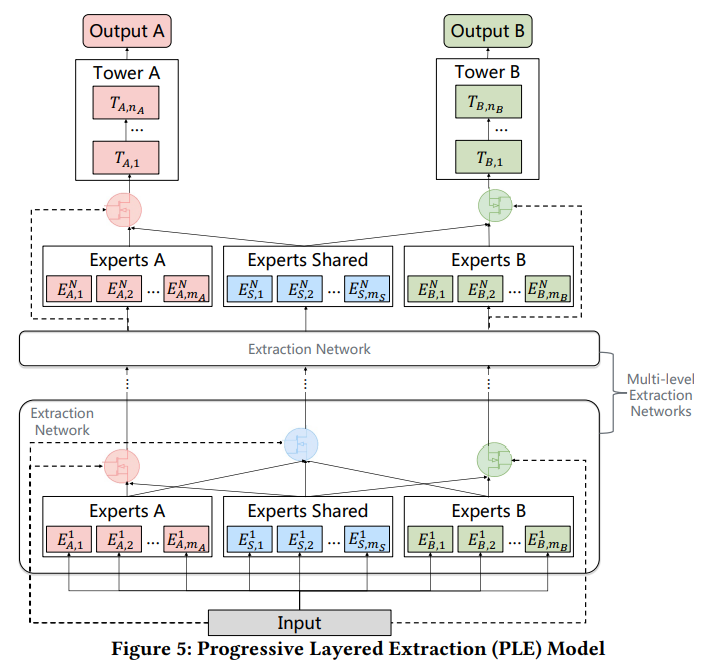
与FM和DeepFM的关系。假设所有字段都是单值的，

从图5中不难观察到，当CIN部分的深度和特征图都设置为1时，xDeepFM通过学习FM层的线性回归权重是DeepFM的一种泛化（请注意，在DeepFM中，FM层的单元直接与输出单元相连，没有任何系数）。

当我们进一步移除DNN部分，并同时使用一个常数和滤波器（简单地对输入求和而不进行任何参数学习）作为特征图时，xDeepFM就降级为传统的FM模型。

实验

在本节中，我们进行了广泛的实验，以回答以下问题：
• (Q1) 我们提出的CIN在高阶特征交互学习中的表现如何？
• (Q2) 在推荐系统中，结合显式和隐式的高阶特征交互是否有必要？
• (Q3) 网络设置如何影响xDeepFM的性能？
在介绍一些基本的实验设置后，我们将回答这些问题。

实验设置

4.1.1 数据集。我们在以下三个数据集上评估我们提出的模型：

Criteo 数据集。这是一个著名的行业基准数据集，用于开发预测广告点击率的模型，并且可以公开访问。给定一个用户和他正在访问的页面，目标是预测他是否会点击给定的广告的概率。
大众点评数据集。大众点评是中国最大的消费者评论网站。它提供各种功能，如评论、签到和商店的元信息（包括地理信息和商店属性）。我们收集了6个月的用户签到活动，用于餐厅推荐实验。给定用户的个人资料、餐厅的属性以及用户最后三次访问的兴趣点（POI），我们想要预测他是否会去这家餐厅。对于用户签到的每家餐厅，我们按照POI的热度抽取了距离3公里以内的四家餐厅作为负样本。
必应新闻数据集。必应新闻是微软的必应搜索引擎的一部分。为了评估我们模型在真实商业数据集上的性能，我们收集了连续五天的新闻阅读服务印象日志。我们使用前三天的数据进行训练和验证，然后使用接下来的两天进行测试。

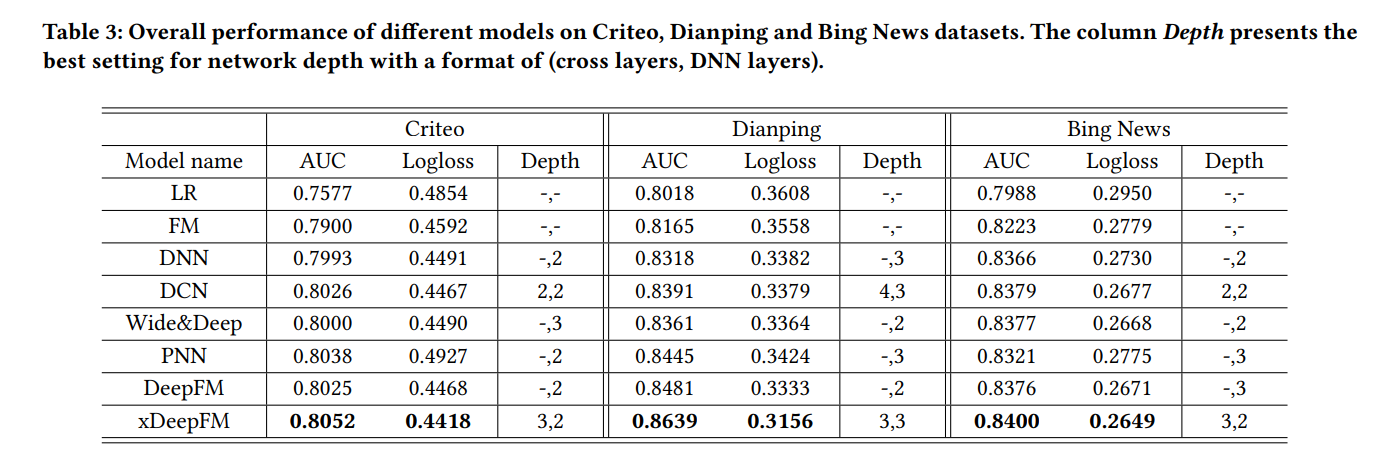
对于Criteo数据集和大众点评数据集，我们以8:1:1的比例随机拆分实例，用于训练、验证和测试。这三个数据集的特点总结在表1中。

基线模型。

我们将我们的xDeepFM与LR（逻辑回归）、FM、DNN（普通深度神经网络）、PNN（从iPNN和oPNN中选择较好的）[31]、Wide & Deep [5]、DCN（Deep & Cross Network）[40]和DeepFM [9]进行比较。正如在第2节中介绍和讨论的那样，这些模型与我们的xDeepFM密切相关，其中一些是推荐系统的最新模型。

请注意，本文的重点是自动学习特征交互，因此我们不包括任何手工创建的交叉特征。