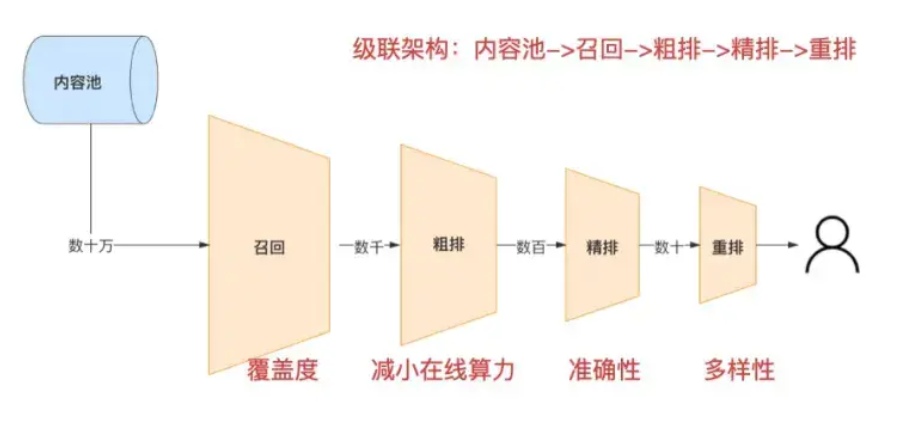
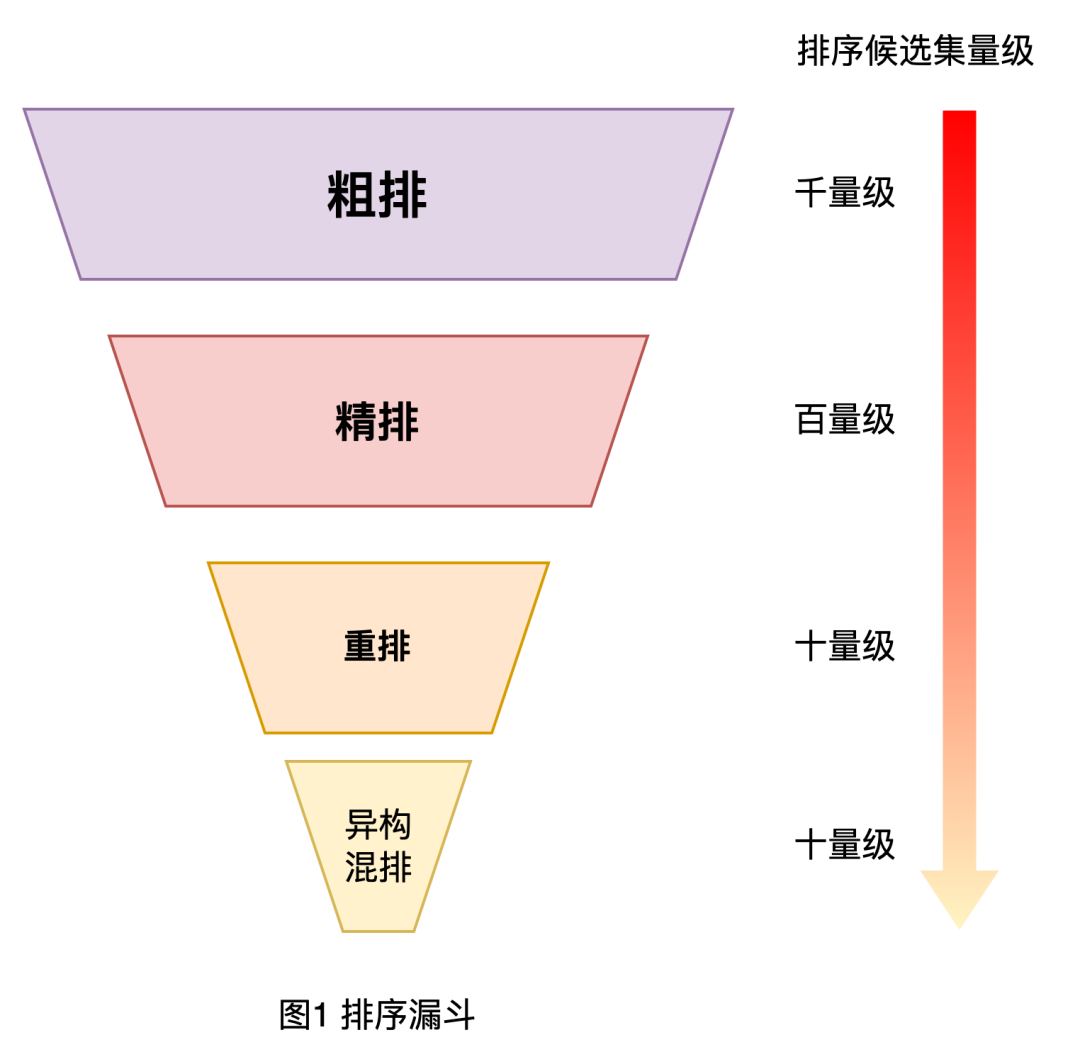
摘要和介绍
作者使用了扩散概率模型,这是一种参数化马尔可夫链,通过变分推理进行训练。这个模型可以在有限的时间内生成与数据匹配的样本。为了学习这个马尔可夫链的转移规则,作者反向操作扩散过程,这个过程实际上是将噪声逐渐添加到数据中,直到信号变得不清晰。作者将这个逆向的扩散过程建模为条件高斯分布,这使得它可以由一个简单的神经网络参数化。
扩散模型的采样过程类似于渐进式的解码,这意味着它逐步生成样本,就像按顺序解码位。通过这种方式,作者能够获得高质量的图像合成结果,并且在评估上取得了良好的分数,包括Inception score分数和FID 分数。这表明这种方法在生成图像方面具有很高的潜力,特别是在处理大型数据集时。
扩散模型 包含的两个过程
前向扩散过程:
反向生成过程
The author used a diffusion probability model, which is a parameterized Markov chain trained through variational inference. This model can generate samples that match the data in a finite amount of time. To learn the transition rules of this Markov chain, the author reversed the diffusion process by gradually adding noise to the data until the signal becomes unclear. The author modeled this reverse diffusion process as a conditional Gaussian distribution, which enabled it to be parameterized by a simple neural network.
The sampling process of the diffusion model is similar to gradual decoding, meaning that it generates samples step by step, like decoding bits in order. In this way, the author was able to obtain high-quality image synthesis results and achieve good scores on evaluations, including Inception score and FID score. This indicates that this method has high potential for generating images, especially when dealing with large datasets.
The two processes included in the diffusion model are:
Forward Diffusion Process: This is the process of gradually transforming a random variable into a Gaussian distribution over time. At each time step, the current variable is mixed with a small amount of noise to create the next variable. This gradually increases the noise in the distribution until it matches the target noise level.
Reverse Diffusion Process: This is the process of gradually transforming a Gaussian distribution back into the original variable. This is done by adding noise to the Gaussian distribution at each time step and removing the noise using an inference network. The inference network is trained to approximate the reverse process of the forward diffusion process and can be used to generate samples from the Gaussian distribution.
背景
- 公式1:逆向过程,被定义成马尔科夫链,从p(𝑥_𝑇 )=𝑁(𝑥_𝑇:0,I)
- 开始学习高斯转换。
Equation 1: The reverse process is defined as a Markov chain starting from p(x_t) = N(x_t; 0, I).
To learn the Gaussian transition.
- 公式2 :扩散模型和其他隐变量模型区别是近似后验(前向/扩散过程)被定义成马尔科夫链,根据变分schedule逐步向数据中添加噪声。
- 公式3 :优化负对数似然函数的变分界限进行训练
- 公式4 :前向过程的显著特性是允许以闭式在任意时间步t采样xt
𝛼t≔1-𝛽_𝑡 , ¯(𝛼_𝑡 ):=∏2(𝑠=1)^𝑡▒𝛼_𝑠
- 公式5,6,7 : 使用SGD优化L的随机项来进行有效训练。通过降低方差来进一步提升,重写L如公式五,公式五通过KL散度去衡量p_𝜃 〖(𝑥〗_(𝑡−1) |𝑥_𝑡)和前向过程后验,当条件是公式6,7。所有的KL散度都是高斯之间的对比,因此可以使用RaoBlackwellized 的闭式表达式计算代替高方差的Monte Carlo估计。
扩散模型和去噪自编码器
- 公式8: 扩散模式看起来是一个受限的潜变量模型,但他们允许很大的自由度。必须选择正向过程方差𝛽_t,模型架构和反向过程的高斯分布参数化。我们建立了扩散模型和去噪分数匹配之间的连接来为扩散模型做一个简单的加权的变分界限目标。
- 前向过程和LT:LT是一个常数,在训练过程中可以忽略
Equation 8: The diffusion model appears to be a variant of a latent variable model with a lot of freedom. It is necessary to choose the variance of the forward process α_t, the model architecture, and the parameterization of the Gaussian distribution for the reverse process. We established a connection between the diffusion model and denoising score matching to provide a simple weighted variational bound objective for the diffusion model.
Forward Process and LT: LT is a constant that can be ignored during training.
- 逆向过程和𝐿_(1:𝑇−1):设置∑2_𝜃▒〖(𝑥𝑡,𝑡)〗, 𝑥_0~𝑁(0,1),𝜇_𝜃 (𝑥_𝑡,𝑡), ,p_𝜃(𝑥(𝑡−1) |𝑥𝑡)=N〖(𝑥〗(𝑡−1);𝜇𝜃 (𝑥_𝑡,𝑡),𝛿_𝑡^2 I),L(t−1) 公式重写如下:
- 公式9,10,11:C是不依赖𝜃的常数,对𝜇_𝜃的参数化就是预测(𝜇_t ) ̃,根据等式4重新参数化来扩展公式8,使用前向过程后验公式7。
- 𝜇_𝜃 (𝑥_𝑡,𝑡)的参数化如公式11
我们能够训练逆向过程均值函数逼近器𝜇_𝜃去预测(𝜇_t ) ̃,或者修改它的参数,我们能够预测∈。
∈_𝜃在Denoising Score Matching 里面是估计的梯度,而噪声∈就是带噪声数据分布的score,即概率密度梯度值。
这个研究中,图像数据被线性缩放到范围[-1,1],由整数组成。这确保了神经网络的反向过程以标准先验分布p(𝑥_𝑇)开始。为了计算离散的对数似然,作者将反向过程的最后一步设置为从高斯分布N(𝑥_0;𝜇_𝜃(𝑥_1,1),𝛿_1^2 I)导出的离散解码器。
这里的D代表数据的维度,i代表提取维度。作者的选择确保了变分界限是离散数据的无损码长,而无需向数据添加噪声或合并缩放操作的雅可比矩阵到对数似然中。
作者还指出,根据逆向过程和解码器的定义,变分界限关于𝜃是可微的。因此,在下面的变分界限上进行训练有助于提高样本质量。
作者还简化了目标函数,去除了公式中的权重因子。这使得加权变分界限更加强调重建的各个方面,相对于标准的变分界限。
最后,作者指出,简化目标函数的扩散模型会减少与小于t的各项损失相对应的权重。这可以使网络在更大的T项中更加专注于更具挑战性的去噪任务。
Here, D represents the dimension of the data, and i represents the extracted dimension. The author’s choice ensures that the variational bound is the lossless code length of the discrete data without the need to add noise to the data or incorporate the Jacobian matrix of the scaling operation into the log-likelihood.
The author also points out that according to the definition of the reverse process and the decoder, the variational bound is differentiable with respect to θ. Therefore, training on this variational bound can help improve sample quality.
The author also simplified the objective function by removing the weighting factor in the formula, which makes the weighted variational bound more emphasizing on various aspects of reconstruction compared to the standard variational bound.
Finally, the author points out that simplifying the objective function of the diffusion model reduces the weight corresponding to the loss terms for smaller t values. This allows the network to focus more on the more challenging denoising tasks among a larger number of T terms.
实验
表1列出了在CIFAR10数据集上的Inception Score、FID分数和负对数似然。当FID分
Progressive coding
训练和测试之间的差距最多为每维0.03位,表明扩散模型没有过度拟合。
扩散模型具有感应偏差,使其成为出色的有损压缩器,因为样本质量很高。
渐进式有损压缩可以通过引入反映方程式形式的渐进式有损代码来进一步研究模型的速率失真行为。
The maximum difference between training and testing is 0.03 bits per dimension, indicating that the diffusion model has not overfitted.
The diffusion model has inductive bias that makes it a excellent lossy compressor because of the high sample quality.
渐进式有损压缩 can be further studied by introducing an iterative equation form of the lossy code.
图五显示了:逆向过程中时间、速率和失真率的关系
在速率畸变图的低速率区域,畸变急剧减小; 这表明大部分比特确实被分配给了难以察觉的失真。
Progressive generation
- 无条件CIFAR 10渐进式生成。从噪声图像到清晰的图像过程。
- 扩展样本和样本质量评估在图10和14中
显示了随机预测x_0~p_0 〖(x〗_0|x_t),对于不同的t,x_t 被冻结。当t很小时,细节被保留下来,t很大时,大的特征被保留下来。
右下角是x_t,其他 来自于p_t 〖(x〗_0|x_t)的采样。
相关工作
研究通过ε-预测反向过程参数化,建立了扩散模型与Langevin动力学之间的联系,为高质量的图像合成和采样提供了新的方法,并在评估中对能量模型领域产生了积极影响。
The research established a connection between the diffusion model and Langevin dynamics by parameterizing the reverse process with ε-prediction, providing a new approach for high-quality image synthesis and sampling, and positively impacting the field of energy-based models in evaluation.
结论
研究揭示了扩散模型与变分推理、去噪分数匹配、Langevin动态、自回归模型和有损压缩之间的联系,对不同数据模态和生成模型具有潜在应用价值,并强调了生成模型的潜在滥用风险。
The research has revealed the connections between diffusion models and variational inference, denoising score matching, Langevin dynamics, autoregressive models, and lossy compression, which have potential applications for different data modalities and generative models. It also emphasizes the potential risk of misuse in generative models.
附录ABCDE
- 神经网络架构遵循PixelCNN + + 的主干,3232模型使用4种特征映射分辨率,256256模型使用6种。作者的CIFAR10 模型有3570 万个参数,LSUN 和CelebA-HQ 模型有114 万个参数。作者还通过增加滤波器计数训练了LSUN Bedroom模型的较大变体,参数约为256 万。
- 作者使用TPU v3-8 (类似于8 个v100 GPU )进行实验。CIFAR 模型以每秒21 步的速度训练,batchsize=128 (10.6 小时训练到800k 步骤),采样一批256 个图像需要17 秒。
- 作者的CelebA-HQ / LSUN (〖256〗^2)模型在batch size=64 时以每秒2.2 步的速度训练,采样128 个图像需要300 秒。作者在CelebA-HQ 上训练了0.5M 步,LSUN 训练了2.4M 步,LSUN Cat 训练了1.8M 步,LSUN Church 训练了1.2M 步,较大的LSUN Bedroom模型训练了1.15M 步。
The neural network architecture follows the PixelCNN++ backbone. The 32x32 model uses 4 feature map resolutions, while the 256x256 model uses 6. The author’s CIFAR10 model has 35.7 million parameters, while the LSUN and CelebA-HQ models have 1.14 million parameters. The author also trained a larger variant of the LSUN Bedroom model with around 2.56 million parameters by increasing the filter count.
The author used TPU v3-8 (similar to 8 v100 GPUs) for the experiments. The CIFAR model trains at a speed of 21 steps per second with a batch size of 128 (10.6 hours to train to 800k steps), and it takes 17 seconds to sample a batch of 256 images.
The author’s CelebA-HQ/LSUN (〖256〗^2) model trains at a speed of 2.2 steps per second with a batch size of 64, and it takes 300 seconds to sample 128 images. The author trained for 0.5M steps on CelebA-HQ, 2.4M steps on LSUN, 1.8M steps on LSUN Cat, 1.2M steps on LSUN Church, and 1.15M steps on the larger LSUN Bedroom model.